So the traditional way to say it is probably 'planar embedding', but I've gone for the alternate terminology of 'squashing flat'. For many molecules, this is a fairly easy process : some decisions have to be made about rotatable bonds, but quite a few drugs are just things sticking off a benzene ring or two.
What is this crazy thing? Well, the other part of the combinatorial map is an 'involution' called α, which is really just another permutation that stores the pair of flags for each edge. In the images above, I have just ordered the edges using the vertices (as 0:1,0:2,0:3,1:2,1:3,2:3) then ordered the flags by vertex index : that is, α = [1, 0, 3, 2, 5, 4, 7, 6, 9, 8, 11, 10].
For fully 3-dimensional molecular graphs (for example) it is trickier. I don't yet know a simple algorithm for choosing different possible embeddings ... er ... squashings. Perhaps they are all complicated; they seem to involve tree data structures with names like "SPQR Tree" (see "Optimizing over all combinatorial embeddings of a planar graph").
Far easier, though, is the intermediate data structure between a graph and some 2D coordinates - known as a combinatorial map. These mathematical objects store the detail of the embedding by recording the order of 'half bonds' called flags (or darts?) around a vertex. Maybe a flag is the vertex and the half-bond. Anyway, here is a picture of K4 (or a squashed tetrahedrane skeleton):
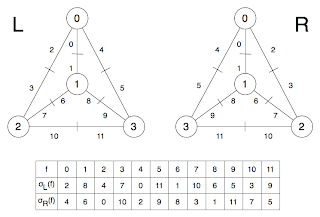
Now the left hand side just shows the graph with labelled vertices, while the one on the right shows the flags (I'm going to call them that now, sorry). At the bottom is the permutation σ applied to the set of flags (f). To understand σ consider just the central vertex (1) : if we travel clockwise round from flag 1, we get the flags (1, 8, 6). In fact, this is how I constructed the permutation : clockwise round all the vertices. It can be helpful to consider σ in cycle notation as (0, 2, 4)(1, 6, 8)(5, 11, 9)(7, 10, 3) which has a cycle for each vertex.This image shows two different embeddings of the same graph. Well, I suppose technically it is different embeddings of the same labelling. In any case, L and R are flipped : if there wasn't so much symmetry it might be better. The same procedure as before is used to get σL and σR (clockwise both times). Now check this out:
What is this crazy thing? Well, the other part of the combinatorial map is an 'involution' called α, which is really just another permutation that stores the pair of flags for each edge. In the images above, I have just ordered the edges using the vertices (as 0:1,0:2,0:3,1:2,1:3,2:3) then ordered the flags by vertex index : that is, α = [1, 0, 3, 2, 5, 4, 7, 6, 9, 8, 11, 10].
Anyway, using the formula φ = σ ⋅ α we get a permutation of what I actually am going to call 'darts'. This is all on the wikipedia page, but it should be clear that the labelled arrows on the image go in cycles. So there is (0, 6, 3) for example. Indeed φ = (0, 6, 3)(1, 4, 9)(2, 10, 5)(7, 8, 11) which is - of course - the four faces of the embedding, including the boundary face.
Phew! Fun stuff, and there is code here as well as some tests here. Well more like just System.out statements, but the beginning of tests...


Comments